Argument of Complex Number

Definition

Given a complex number \(z - \{0\}\), the principal argument of \(z\) is defined an the real number \(-\pi < \theta \leq \pi\) such that

\[ z = r (\cos(\theta) + i \sin(\theta)).\]

We write \(\mathrm{Arg}(z) = \theta\).

Geometrically, the argument represents the angle, measured from the positive real axis, that \(z\) forms on an Argand diagram.

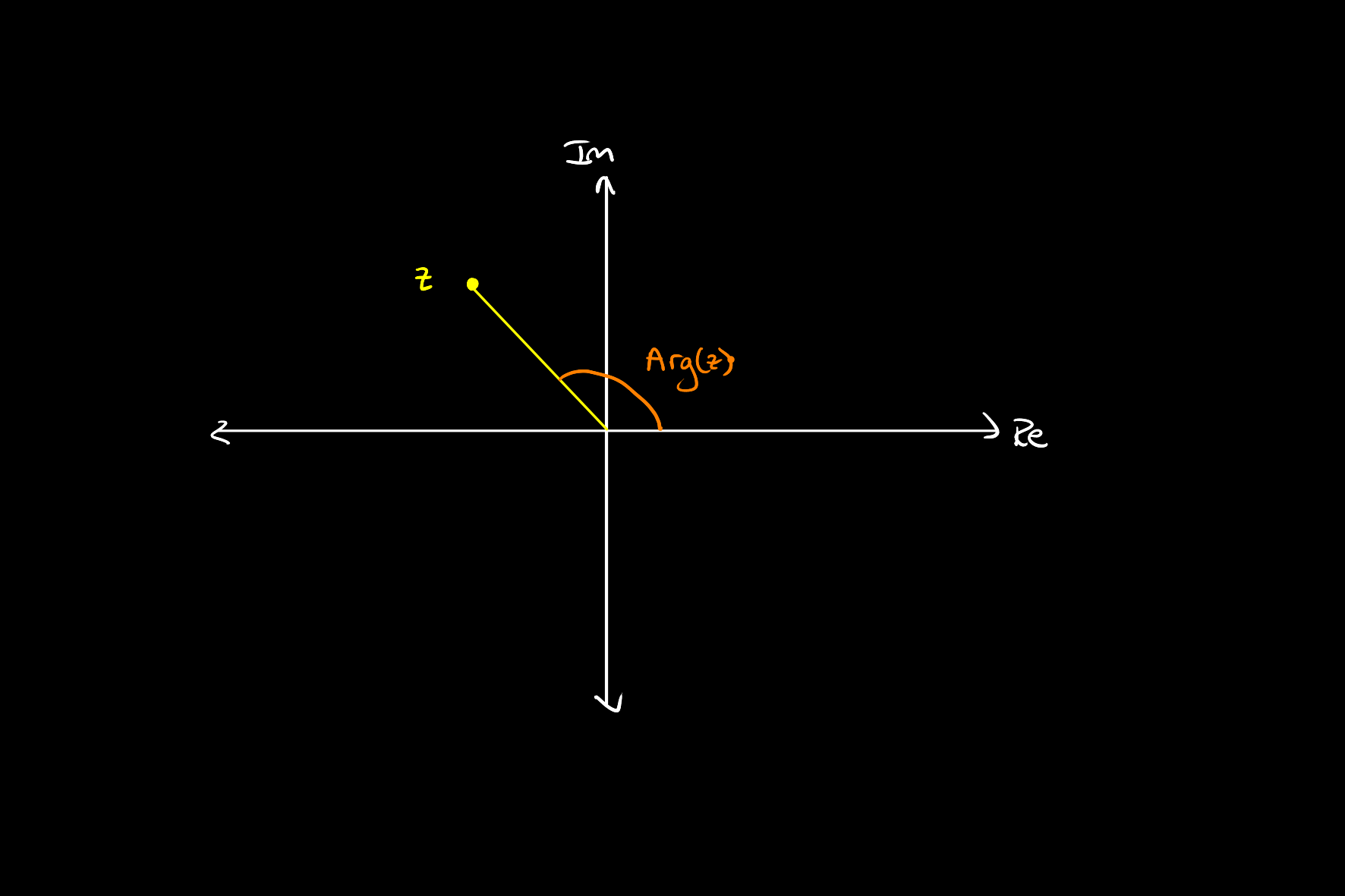
More generally, we write \(\arg(z)\) to either represent the set of choices for \(\theta\) as above, or for a particular arbitrarily chosen value. However, the somewhat less common notation of \(\arg_\theta\) for the argument satisfying \(\theta < \arg_\theta (z) \leq \theta + 2\pi\) is very useful.

Theorem

\[ \arg_\theta (z) = \mathrm{Arg}(z) + 2n\pi\]

for some \(n \in \mathbb{Z}\).

This result, along with the fact that the principal argument is uniquely defined, follow from the equivalent fact from polar coordinates.